Rigorous statistics are often at odds with the needs of modern, product-driven companies to move fast and ship fast. Statistics are all about probabilities, and the more data, the better the accuracy of the predictions. Product led organizations are all about building the smallest part of a project which can add value as fast as possible, and then iterating quickly, looking for signals of product market fit. The Venn diagram of these two areas overlap with A/B testing, but this creates a tension between the statistics and the need to move fast.
If we all had enormous amounts of traffic to test against, and infinite time to do these tests, we would make almost perfect decisions. Realistically, pressures of shipping fast often cause us to make calls on less than perfect data. These pressures can happen when metrics appear to be doing especially well or poorly, or if there are time constraints. You can, of course, stop a test whenever you like, as long as you’re aware of what this does to your statistics.
User behavior data has a lot of random variation, and this creates a noisy signal (it’s also a reason why trend data — data over time — is largely meaningless in A/B testing contexts). If samples are small you’re more likely looking at noise than if samples are large. The more sample sizes increase, the more this noise is averaged out. Furthermore, if you’re using a Frequentist approach, your statistics only become actionable when the predetermined sample sizes are reached — otherwise you’re falling into the peeking problem, the subject of many articles. If you’re using statistics which are less susceptible to peeking, like Bayesian or Sequential, you can peek and make decisions.
In all these contexts, some data is absolutely better than no data, but without finishing a test you increase the odds of picking the wrong variation, and you lose the resolution on the most probable outcome. In short, you increase the risk of making a decision. The question that every experimentation program should be asking then is, what is your appetite for risk?
Risk
Most A/B testing statistics give you the chance to beat baseline/control as the probability that your variation is at least better than other control variation. But this measure gives no indication as to the amount better or worse it will be. If you’re forced to make decisions without perfect data, wouldn’t it be great to have some indication of what risks you’re taking? You would like to know, if you call the test now, and you’re wrong about which variation you implement, what the likely negative impact would be. The good news is that Bayesian statistics give us just such a measure.
This risk, also known as potential loss, that Bayesian statistics provide can be interpreted as “When B is worse than A, if I choose B, how many conversions am I expected to lose?” It can replace the P-value as a decision rule, or stopping rule for A/B testing — that is, you can call your tests if the risks go below (or above) your risk tolerance thresholds, instead of using other values. If you want to read more about how risk is calculated, you can read Itamar Faran’s excellent article: How To Do Bayesian A/B Testing at Scale.
Growth Book recently implemented this same risk measure (with the help of Itamar) into our open-source A/B testing platform. This measure empowers teams to call tests earlier and be aware of the risks they are taking in doing so.
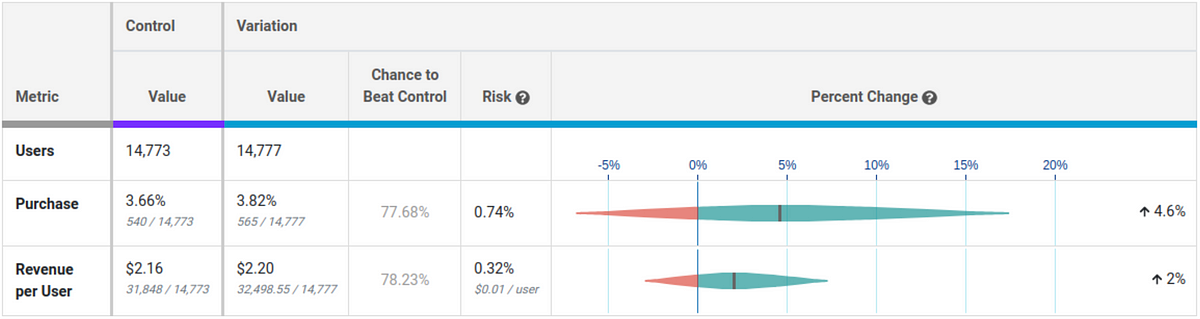
In the above example, both metrics are up, but only have about a 78% chance of beating the control, well short of the typical 95% threshold. However, neither one appears to be very risky. If you stop the test now and choose the variation and you’re wrong, your metrics would only be down less than a percent. Depending on your business, that may be good enough and you can move onto the next experiment without wasting valuable time.
The combination of Chance to Beat Control, Risk, and a Percent Change confidence interval gives experimenters everything they need to make decisions quickly without sacrificing statistical accuracy.







