Multi-Arm Bandit testing comes from the Multi-Arm Bandit problem in mathematics. The problem posed is as follows: given a limited amount of resources, what is the best way to maximize returns when gambling on one-arm bandit machines that have different rates of return? This is often phrased as a choice between “exploitation,” or maximizing return, and “exploration,” or maximizing information. When applied to A/B testing it can be a valuable tool. In this article I’ll go into more details as to what multi-arm bandit testing is, how it compares to A/B testing, and some of the reasons you should, and should not, use it.
What is Multi-Arm Bandit testing?
Imagine you walk into a casino and you see three slot machines. In this hypothetical casino, there is no gaming control board to guarantee that each machine has the same return. In fact, you’re fairly certain that one of the machines has a higher rate of return than the others. How do you figure out which machine that is? One strategy is to try and figure out the return for each machine before spending the majority of your money. You could put the same amount of money into each machine, and compare the return. Once you’ve finished you’ll have a good idea of which machine has the highest return, and you can spend the rest of your money (assuming you have any) on it. But while you were testing, you put a fair amount of money into machines which have a lower return rate. You have maximized certainty at the expense of maximizing revenue. This is analogous to A/B testing.
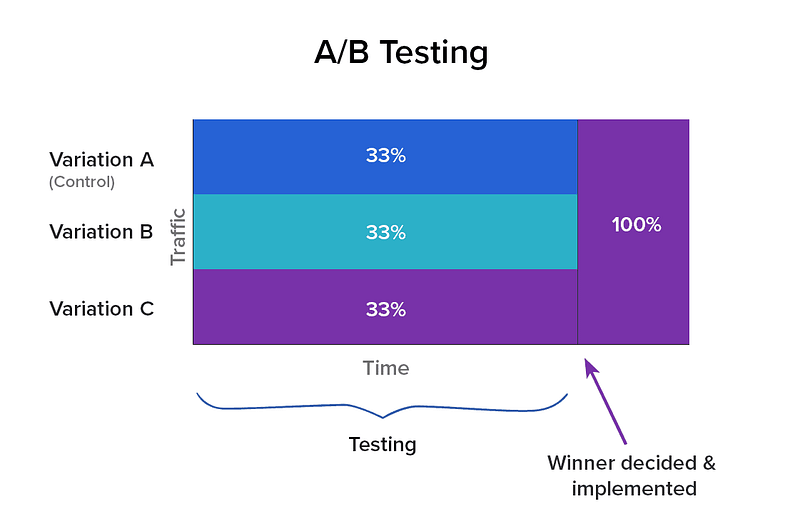
There is a way, however, to maximize revenue at the expense of certainty. Imagine you put a small amount of money in each machine, and looked at the return. The machine(s) that returned the most, you place more money into the next round. Machines that return less, you put less money into. Keep repeating and adjusting how much money you’re putting in each until you are fairly certain which machine has the highest return (or until you’re out of money). In this way you’ve maximized revenue at the expense of statistical certainty for each machine. You have avoided spending too much money on machines that don’t have good returns.
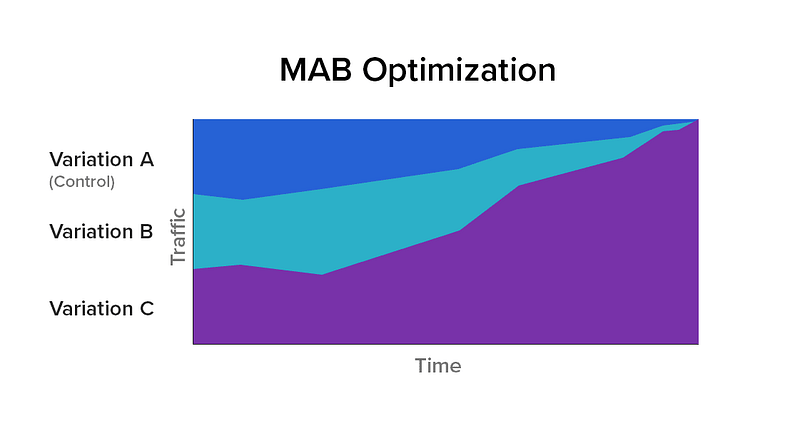
This is the premise behind Multi-Arm Bandit (MAB) testing. Simply put, MAB is an experimental optimization technique where the traffic is continuously dynamically allocated based on the degree to which each variation is outperforming the others. The idea is to send the majority of the traffic to variations that work well, and less to those that are performing poorly. What MAB guarantees is that, unlike an A/B test, during the course of the test, the total number of conversions will be maximized. However, because the focus is on optimizing conversions as a whole (inclusive of all variations), you lose the specifics about each.
The main advantages are that you can avoid sending traffic to test cases which aren’t working, optimize page performance as you test, and introduce new test cases at any time. Sounds great, right? However, this kind of testing is not ideal for all situations. Let’s take a look at situations where MAB is appropriate, and where it isn’t.
Problems with Multi-Arm Bandit testing
Multiple metrics and unclear success metrics
If you are using multiple metrics for the success of your experiment, MAB is usually not the right test. If a variation has one metric that increases, and another that decreases, how do you know how much traffic to send to it? Even if you do have one main metric you’re using to determine success, you’ll want to also include your guardrail metrics (metrics which you include in all tests to make sure you’re not doing something bad, like cannibalizing traffic, or increasing page load time, which might hurt SEO in the long term). Often tests require some interpretation to determine which variation you want to go with. You might even decide you’re okay with one metric losing because of some longer-term gain in mind. With MAB, you’re handing over the decision-making to the algorithm.
Variable conversion rates
Multi-Arm Bandit testing assumes that conversion rates are constant over time. For example, if one cohort of your traffic converts better on the weekends, but not so well during the week, the variation which gets the most traffic will depend on when you start the test. This will either cause a false positive, or seesawing of the traffic to variations. You can avoid this by making sure your algorithm for allocating traffic takes these time variations into account — assuming you know what they are.
Conversion windows
Conversion windows pose another problem. The usual algorithm expects conversion events to happen fairly immediately after the user sees a variation; after all, it’s using these conversions to allocate traffic. If there is a delay between a user seeing a variation and the conversion event, this could cause the MAB algorithm to incorrectly distribute traffic.
Simpson’s Paradox
Because with MAB you’re not exactly sure why a variation is better than the others, and you don’t have detailed statistics on the performance of each variation, you open yourself up to the Simpson’s Paradox. The Simpson’s Paradox as it applies to A/B testing is an interesting one, and probably a topic of another article. Simply put, Simpson’s Paradox with testing can result in one variation winning on aggregate, but actually losing if the traffic is segmented differently. Since you don’t have the detailed statistics to dig into, you may be more likely to fall into this situation.
Time and complexity
Setting up MAB tests tends to be more complicated than A/B tests. This complexity increases the error rates. You’ll need to have a lot of trust in your algorithms to make decisions based on the results they produce. MAB tests also take longer to decide on a winner which will get all the traffic, and you may not want to wait that long.
When to use Multi-Arm Bandits
Exploratory tests
The one situation where MAB testing is very useful is for exploratory tests without a real hypothesis — like Google’s 41 shades of blue test. Google employees couldn’t agree on which color of blue would be best. They initially decided on a compromise color, but then decided to test to find which colors caused users to click more. They didn’t really have an idea of which shade would be best, but they thought there might be a difference, so why not test it. [I do not believe Google used a Bandit for that specific test, but this kind of optimization test aligns well for its use. They claim it resulted in an extra $200M a year in revenue. I believe the successful blue was #1A0DAB.]
Independent tests
If you can select one metric, and you are certain that the metric in the area you’re testing is independent from other metrics, MAB testing can work out well. However, this situation is rare. Metrics of user interactions tend to be highly interdependent and hard to isolate. One example of where you might find independent variables is in search marketing landing pages, where the traffic has not experienced your product before, and you can shape their experience without affecting other traffic or flows.
In a rush
There are situations where you want to deliver the best experience to your users, but don’t have time to do a full A/B test, or the context is temporary, such as a promotion or topical event. In these cases, maximizing your conversions is more important than being statistically perfect. You might consider adding all variations into a bandit and letting it run. You can also add and adjust variations as often as you like and let the algorithm adjust the traffic to the best version.
Contextual Bandits: MAB with personalization
Imagine you have 20 possible headlines for a page and want to optimize conversions. A traditional MAB test is winner takes all — whichever headline performed the best across all users would win. But what if younger users prefer headline C and older users prefer headline D? Your experiment doesn’t take age into account so the result would be suboptimal. If you thought age was really important, you could design a multivariate test up front, but that approach doesn’t scale well once you start adding a lot of dimensions (country, traffic source, gender, etc.). Contextual Bandits solve this limitation by maximizing for all possible permutations.
For many use cases, Contextual Bandits can give you the best possible conversion rates. But this comes with a cost. Unlike MAB or traditional A/B tests, you don’t end up with a single “winner” at the end of a Contextual Bandit experiment. You instead end up with complex rules like “young Safari visitors from Kentucky see headline B.” Besides being hard to interpret, imagine doing this on multiple parts of a page — you’ll quickly end up with thousands of possible permutations. This results in either much longer QA or a lot more hard-to-reproduce bugs. From my experience, this cost usually outweighs the benefits for most use cases.
Conclusion
Multi-arm Bandits are a really powerful tool for exploration and generating hypotheses. It certainly has its place for sophisticated data-driven organizations. It is great for regret minimization, especially if running a short-running campaign. However, it is often abused or used for the wrong experiments. In real-world use, there are some cases where MAB is not the best tool to use. Decisions involving user performance and data are nuanced and complicated, and giving an algorithm a single metric to optimize and removing yourself completely from the decision-making process is asking for trouble in most cases. Usually hypothesis-based testing leads to superior results. You’ll end up with the ability to dig into the data to understand what is happening in each test variation, and use this to uncover new test ideas. Experimenting this way leads to cycles of testing that are the hallmark of successful A/B testing programs.







